Wishing upon a star

When I was a boy, many years ago…

…I used to like building polyhedron models out of card. Here is a photo of me, probably around 1987ish, spray-painting a compound of ten tetrahedra. Evidently the photographer had partially obscured the aperture with their finger, but there were no digital cameras back in those days, you only found out your mistakes when you had the picture developed!

Making a model out of card was a long and laborious process. First, armed with a protractor and ruler, one had to draw the net on card, making sure there were tabs in the right place to glue the thing together. Then it had to be cut out, and the intended folds scored very carefully with a craft knife (you need them to fold cleanly, but if you cut through the card you’ll have to start again). Finally, it had to be glued together to give it three-dimensional form, a process which got increasingly fiddly as access to the interior became harder.

This being the season of goodwill and all that…

…I thought I’d make a Christmas star decoration out of card. My plan was to make what was essentially an icosahedron but with pointy triangular pyramids on each face (a bit like a stellated icosahedron). I figured that I could save time on the net construction by creating them in SVG and laser-printing them onto card. I scribbled onto a convenient piece of paper my plan for the net:

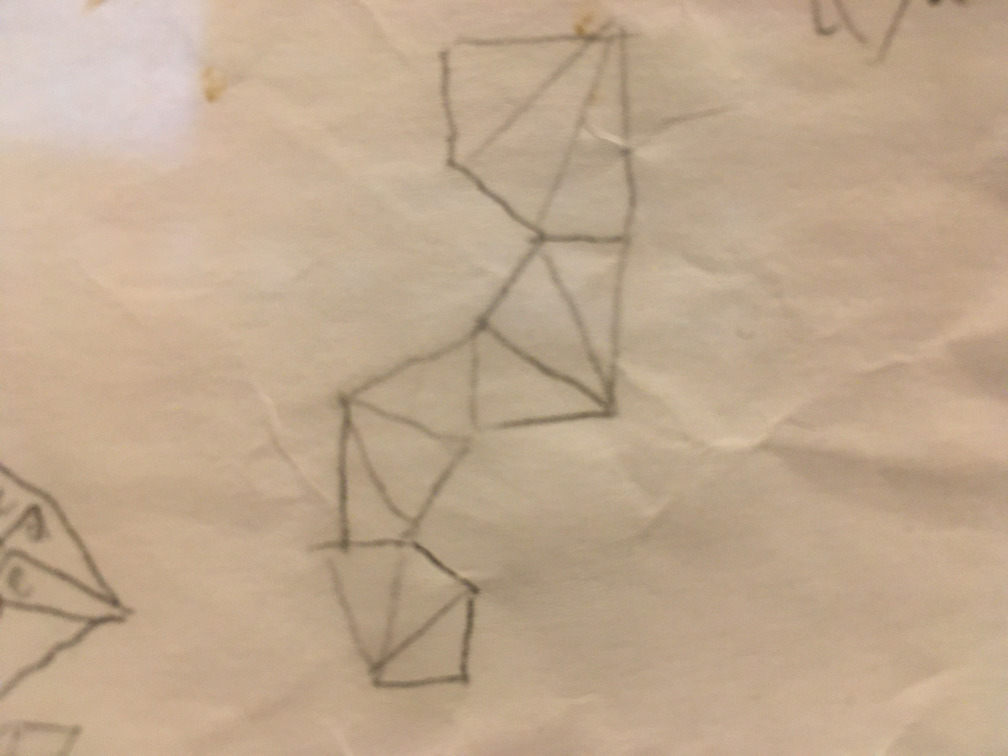
One of those, I figured, would fold to make a chain of four pyramids, and five such chains could be joined together to make the final shape. The big question was – how pointy should I make the pyramids? Too pointy, and they’d be really tricky to glue together. Not pointy enough and the star would look a bit rubbish. Also, I needed to make each net as big as possible while still being printable onto an A4-sized piece of card. I could obviously prototype this by drawing something in Inkscape, but I didn’t fancy the faff of having to edit it and make sure all of the angles came out right. So, naturally, I started to wonder how I could write something to generate the SVG for me, allowing me to tweak angles and regenerate at will (it didn’t have to solve the problem completely; I could always scale and rotate in Inkscape to make best use of the card).

Cometh the hour…

…cometh the libraries. Two of them, in fact. To handle the geometry, I remembered that years and years ago I’d written a silly math library in Java, and happily I’d written something similar in Scala (neither of these is to be taken seriously as a proper library – do not use them!). That handles points, vectors, lines and so on. But then I wanted a way to describe the net in terms of “this is how you make a triangle with a base angle of x degrees, so draw one, rotate a bit, draw another one, now do another of these shapes but flipped…” and so on.

Basically, this would be something a bit like Logo, where there’s a notional “turtle” that exists on the plane somewhere, and can be told to go forward, or turn through some angle, with a pen that’s either down or up so it may or may not draw a line when it moves. So at any moment, there’s some “state” in the system (the set of lines drawn so far on the canvas, the location and orientation of the turtle) and I want to be able to issue commands that update the state or rather, since this is Scala, we want the state to be immutable and commands will return an updated copy of it.

So a first stab (in pseudocode) at something to draw an isoceles triangle with a particular base length and opposite angle might look something like this:

def triangle(currentState: State, baseLength: Double, oppositeAngle: Rad): (State, Point) {
  val equalAngle: Rad = (Rad.PI - oppositeAngle) / 2.0
  val equalSide = baseLength / (2 * Math.cos(equalAngle))
  val currentlyFacing = getCurrentDirectionFromState(currentState) // because we'll want to use this later
  val (stateAfterDrawingBaseLine, endPointOfBaseLine) = drawLineAndMove(currentState, baseLength)
  val stateAfterRotatingTheFirstTime = rotateBy(getCurrentDirectionFromState, Rad.PI - equalAngle)
  val stateAfterDrawingTheFirstEqualSide = drawLineAndMove(stateAfterRotatingTheFirstTime, equalSide)
  // ... you get the idea
} yield endOfBase

There are at least three problems with this approach:

1. We keep having to return an updated state, which needs to be passed on to the next instruction for it to operate on, which means we have to get creative with variable names. I could have used state1, state2, state3 and so on, but it’s still a bit ugly, and easy to use the wrong state somewhere leading to mysterious bugs.
2. Sometimes we want to return something additional to the new state (e.g. the end point of the line we’ve just drawn). We can either invent a bunch of case classes for this, or return a Tuple(State, something else), but the lack of uniformity of return types seems a bit inelegant.
3. We’re not handling errors anywhere.

We can do something about “3” easily, at least – if we define methods to return Try[(State, other, things)] then we can use a for-comprehension and potentially deal with errors using the usual .recover, .recoverWith combinators. But the first two issues still rankle.

The second library…

…and the subject of this blogpost after an extended scene-setting introduction, is a library for sequencing computations (internal to 67 Bricks, I’m afraid, so no link!) which I wrote a few years inspired by exercises in the book Functional Programming in Scala (looking around my office, I can’t see it anywhere, which makes me wonder if I lent it to someone).

Let us cut to the chase, and see what the triangle method looks like, and then try to understand it.

def triangle(baseLength: Double,
             oppositeAngle: Rad): Computation[Canvas, Point, DrawFailure] = {
  val equalAngle: Rad = (Rad.PI - oppositeAngle) / 2.0
  val equalSide = baseLength / (2 * Math.cos(equalAngle))
  for {
    facing <- getFacing
    endOfBase <- drawLineAndMove(baseLength)
    _ <- rotateBy(Rad.PI - equalAngle)
    _ <- drawLineAndMove(equalSide)
    _ <- rotateBy(Rad.PI - oppositeAngle)
    _ <- drawLineAndMove(equalSide)
    _ <- moveTo(endOfBase)
    _ <- rotateTo(facing)
  } yield endOfBase
}

So, it is a for-comprehension, and it’s all quite easy to follow, but where on earth has the state gone? There’s no state being passed into the method, and we appear to be ignoring the return values from many of the methods (assigning to _). And what is that Computation[Canvas, Point, DrawFailure]?

Computations, and their outcomes

The computation library has a trait Computation[S, +A, +F], and a sealed trait ComputationResult[S, +A, +F] defined as follows:

trait Computation[S, +A, +F] {

  def run: S => ComputationResult[S, A, F]

  def map[B](fn: A => B): Computation[S, B, F] = ... // details omitted

  def flatMap[B, G :> F](fn: A => Computation[S, B, G]): Computation[S, B, G} = ...

}

object Computation {

  private class ComputationImpl[S, +A, +F](override val run: S => ComputationResult[S, A, F]) extends Computation[S, A, F]

  // Constructor for Computations, transforming a suitable function into a Computation
  def apply[S, A, F](run: S => ComputationResult[S, A, F]): Computation[S, A, F] = new ComputationImpl(run)

}

sealed trait ComputationResult[S, +A, +F]

case class Ongoing[S, +A, +F](state: S, result: A) extends ComputationResult[S, A, F]

case class Failed[S, +A, +F](error: F) extends ComputationResult[S, A, F]

A Computation[S, A, F] is basically a function, which takes some kind of “state” (represented by the type S), and must return a ComputationResult of which there is a choice of two; either an Ongoing encapsulating an updated state S and possibly some kind of observable result of type A, or a Failed which holds an error of type F. In the triangle example above, we have the following:

• The “state” was a class called Canvas which basically holds a list of all lines drawn so far plus the current location and orientation of the “turtle”
• The return type of that particular function (the A) was Point, being the point at the end of the baseline of the triangle
• The “error” type was a case class called DrawFailure (which was basically a wrapper around a Throwable)

So where is the state in the triangle function? Where does the drawing happen? The answer is that the triangle function by itself doesn’t really do anything immediately when it is called. The Computation[Canvas, Point, DrawFailure] it returns can be thought of as function which, when called with a suitable Canvas, will return an updated Canvas with the lines of a triangle drawn on it. Since it has been written as a for-comprehension over other Computations, it doesn’t immediately look like it’s a function, and neither do the things it calls, and in fact we have to explore a little way into the nest of Computation-returning functions until we find something that isn’t implemented as a for-comprehension but actually looks like it contains a function, for example:

def addLine(newLine: Line): Computation[Canvas, Unit, DrawFailure] = Computation(c => Ongoing(c.addLine(newLine)), ())

This, finally, returns a function which, when called with a Canvas, will call the addLine method on Canvas (which returns an updated Canvas), and parcels this up in an Ongoing with Unit (()) as the return value.

The things that makes the magic happen are the map and flatMap functions defined in the Computation trait, the existence of which enables the use of for-comprehensions. The map method simply allows the return type of the Computation to be changed from A to B, given a function A => B. If you had a Computation[S, String, F] you could append .map(_.length) to convert it to a Computation[S, Int, F] returning the length of the computed String but not changing the state in any way (or the fact that the result was Ongoing). The flatMap function is more powerful; it allows a new Computation to be created based on the returned result (the A) of the current Computation.

Why use the library?

The example above was basically a bit of fun – a case of me finding uses for a couple of things I’d previously written, hacking something together to solve a problem. The final code used to create the net looked something like this, where fan drew a three-triangle structure like the structure at the top of my sketch above:

val baseLength = 100.0
val baseAngle = Rad.PI / 6

val doFan =  fan(baseLength, baseAngle, 3)

val twoFans = for {
  _ <- doFan
  _ <- rotateBy(Rad.PI)
  _ <- doFan
} yield ()

val program = for {
  _ <- moveTo(Point(105.0, 148))
  _ <- twoFans
  _ <- moveBy(-baseLength)
  _ <- twoFans.flipped
  result <- getResult
} yield result

Writing the individual parts of this as computations made them really easy to combine, and easy to think about. I think that if this had been written in an imperative style (mutating the Canvas as we go along), or using something like the Try or Either monad in a for-comprehension, it would have been quite complicated to make all the parts fit together nicely. As it is, because passing around the state is taken care of behind your back there’s much less clutter in the code, and it’s very easy to build up a complicated Computation out of smaller parts.

The initial impetus for writing the computation library was when I was writing something to handle serializing arbitrary objects as Strings through the use of the typeclass pattern. I modeled the parsing of a String as a state containing the String being parsed, and the index of the character being processed; it was then possible to implement simple computations (e.g. “read a character”, “read a character that is expected to be a digit”) and build up via intermediate computations (“read an Int, then read a ‘|’, then read that many characters”) to complicated things (“to read a List[Foo], run the computation to read a Foo repeatedly until it fails”).

I would certainly recommend the challenge of writing such a library; it’s not too difficult (the Computation and ComputationResult traits above might be a useful basis), and the mental exercise involved is stimulating. When you have something working, you can try adding additional combinators to Computation e.g orElse to try running the current computation falling back to an alternative if it fails. In use, you may find it helps to use type aliases (e.g. in my “star” project, I used DrawComputation[T] as an alias for Computation[Canvas, T, DrawFailure] and a DrawComputation object with an apply method for “bootstrapping” the low level computations e.g. addLine).

…and how did the star turn out?

I was quite pleased with the end result. After fiddling with parameters, and figuring out how to generate the appropriate SVG (another long story…) I settled on the following net.

Here are the nets cut out and partially scored:

…and here the final star, after being sprayed gold and having its tips spread with glue and dipped in glitter.

Merry Christmas!